Unrelated, but fairly awesome.

http://gizmodo.com/5850643/what-the-hell-magnets-why-are-you-so-amazing?tag=science

http://andrewsullivan.thedailybeast.com/2011/11/ment-5.html

Series and Parallel Circuits

Circuit problems

1. 10 coulombs of charge flows past a point in a circuit in 4 seconds. What is the current?

2. A 50-ohm resistor is connected to a 10-volt battery. What current passes through the resistor?

3. Two 100-ohm resistors are in series. What is their total resistance?

4. If these two 100-ohm resistors were connected in parallel, what would be their total resistance now?

5. Work out problems 3 and 4, assuming that the resistors are connected to a 10-volt battery. Draw diagrams for each situation, and find the total current in the circuit.

What exactly *IS* a circuit?

An electrical circuit can be thought of as a complete "loop" through which charge can travel. Therefore, it actually has to be physically complete - there can be no openings. That is, the current actually has to have a full path to take.

But there is an exception:

If the supplied voltage is high enough, charge can "jump" an "open circuit." This is clearly a dangerous situation, and one way in which a person can get shocked. Think of the unfortunate situation of sticking your finger (or a paper clip, etc.) into an electrical outlet (or something like a toaster, for that matter). You would "bridge" the circuit, becoming in effect, a resistor.

That's bad.

Electrical Currents

Thus far, we have discussed static charges. Static charges alone are useful, but not nearly as much as charges in motion. As you recall, electrons are most easily moved. However, for sake of ease in sign convention (keeping things positive, where positive), we define the following:

current (I) - the rate at which positive charge "flows"

I = Q/t

The unit is the coulomb per second, defined as an ampere (A). One ampere (or amp) is a tremendous amount of current - more than enough to kill a person. In fact, you can feel as little as 0.01 A. Typical currents in a circuit are on the order of mA (milliamperes).

We also define other new quantities in electricity: voltage, resistance, power

voltage (V) - the amount of available energy per coulomb of charge

V = E/Q

resistance (R) - the amount by which the voltage is "dropped" per ampere of current

R = V/I

You can also think of resistance of that which "resists" current. Typically, resistors are made of things that are semi-conductors (they conduct current, but less well than conductors, and better than insulators). Resistors are often made of carbon, but can also be made of silicon and other materials. The unit is a volt per ampere, defined as an ohm (Greek symbol, omega).

A convenient way to relate all the variables is embodied by Ohm's Law:

V = I R

As in, "Twinkle, twinkle little star, V is equal to I R."
Well, it works for me.

Electrostatics questions

1. What is the difference between an electron and a proton: in terms of charge? In terms of mass? In terms of position in an atom?

2. By "charging" something, what is usually happening? If the object is becoming negatively charged? Positively charged?

3. What is the charge of a proton? An electron?

4. Knowing the charge of one proton, how many protons would be required to make one coulomb of charge? This will be a large number.

5. Explain the rotating meter stick demonstration (similar to how a balloon sticks to a wall).

6. What is a Van de Graaff generator?

7. What is "grounding?"

8. What do you suppose occurs when lightning strikes?

9. What happens to the electrostatic force between two charged objects if the distance between them is doubled? Tripled? Halved?

10. What do we mean by "fundamental" charge? What charges are fundamental?

Astronomy images FYI

http://www.panoramas.dk/fullscreen3/f2_mars.html
View QTVR

http://hubblesite.org/

http://hubblesite.org/gallery/

http://apod.nasa.gov/apod/

http://www.nasa.gov/multimedia/imagegallery/

http://www.youtube.com/watch?v=6A3XGzkcDUA&feature=youtu.be




Also, for your interest:

http://lightyears.blogs.cnn.com/2011/11/26/giant-mars-rover-set-for-launch-saturday/?hpt=hp_t2

Static electricity

Charge
As fundamental to electricity and magnetism as mass is to mechanics

Charge is a concept to quantitatively relate particles to each other, in terms of how they affect each other. Charge is represented by Q.

The basic idea - like charges repel (2 negatives or 2 positives). Opposite charges attract.

Charge is measured in terms on units called coulombs (C). A coulomb is a huge amount of charge.

The charge of a proton is tiny: 1.6 x 10^-19 C.

Similarly, the charge of an electron is the same value but negative (by definition): -1.6 x 10^-19 C

The Charge of a neutron is 0 C, or neutral.

How particles interact with each other is embodied in a physical law called Coulomb's law:

F = k Q1 Q2 / d^2

Or, the force tha exists between 2 particles is proportional to the product of charges divided by the distance squared. A proportionality constant is used to make units work out nicely.

Note that this is an inverse square law like gravitation.

The big 3 of particles are:

Proton
Neutron
Electron

However, of these onl the electron is "fundamental," meaning that it can't be further subdivided. Protons and neutrons can be broken up into quarks.

There are 6 types of quarks - up, down, top, bottom, charm, strange. The names mean nothing.

They are exotic particles which typically do not exist alone in nature.

A proton is: 2 ups and a down quark.
A neutron is: 2 downs and an up quark.

Well over 100 particles exist, but few are fundamental.

Diffraction and Holography

When light passes through small openings or around barriers, it can actually interfere with itself - this is called diffraction. Like interference, patterns can result - and these patterns are related to the opening or barrier that caused the diffraction.

Holography is an interference phenomenon, caused by two beams - a reference beam, coming from the laser, and an object beam (which reflected off the object). This interference pattern is burned into the film emulsion of holographic film. It can be reconstructed when light passes through it again.

Interference and Diffraction

Consider 2 waves meeting each other in the same space. Their energies (AKA wave amplitudes) can add (or subtract). This phenomenon is called interference. If you've ever added sine waves on a calculator before, the effect is similar - and sometimes also called superposition.

Crests can add to other crests or cancel with troughs - however, it's usually some combination, depending on the waves in question. And often, beautiful "interference patterns" can result.

Optics Problems

1. Describe what happens to a light ray as it enters a piece of glass (or tank of water, for that matter) -

a. at a zero degree angle (with respect to the normal)

b. at a non-zero angle

(Though the math may be less comfortable to you, a relationship called Snell's law describes this all perfectly.)

2. Describe the law of reflection.

3. What exactly is the focal length of a lens or mirror? Under what circumstances are images formed AT the focal point?

4. Does a flat/plane mirror have a focal length? Discuss.

5. What is the difference between real and virtual images?

6. In the lens equation, there are 3 relevant variables. What are they?

7. Draw what happens when several parallel rays of light hit:

a. convex lens

b. concave lens

c. concave mirror

d. convex mirror

e. plane mirror

8. "An image always forms at the focal length of a lens or mirror." This statement is false for more than one reason. Discuss.

9. A convex lens is similar to a _____. Why?

10. A concave lens is similar to a ______. Why?

11. With a convex lens, a real image is formed everywhere except when the do is _____.

12. When the do is between f and 2f, the images are always _____.

13. When you are using a magnifying glass or make-up/shaving mirror, where are you placing the object (do) to get a magnified image? What type of image is this?

14. What types of lenses are used for nearsightness and farsightedness?

The Lens/Mirror Equation

1/f = 1/di + 1/do

In this expression:

f - the focal length of the lens or mirror; that theoretical point where light rays converge ONLY if they were initially parallel. In practice, this is where the light rays from the Sun would meet through a convex lens or concave mirror

A positive (+) focal length indicates that the optic can converge light (convex lens or concave mirror). A negative (-) focal length indicates that the optic can NOT converge light (concave lens or convex mirror).

do - the "object distance," or distance between object and lens or mirror

di - the "image distance," or distance between the formed image and lens or mirror

If you do the calculation for di and it is negative, the image is virtual. Otherwise, the image is real.

Mirrors

Optics - Camera and Eye

Lenses - concave and convex

A few practice problems

.... from the text:

268-9: exercises 8, 10, 16, 36-49; problems 3, 5, 6

291-2: exercises 2, 3, 5, 6; problem 1

315-6: exercises 12, 18, 19, 22

Don't forget to review problems related to these concepts:

strings/harmonics
organ pipes / harmonics
music - octaves, piano keys (half-steps)
index of refraction

And be sure to review all topics listed in the earlier post, as well as all relevant blog postings. For confusion, also feel free to send questions to:

Dana Molloy
dana.j.molloy@gmail.com

She is a Towson physics major who may be able to help if I can not get back to you quickly.

Good luck!

Lenses

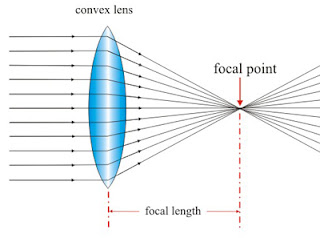
As shown and discussed in class, light refracts TOWARD a normal line (dotted line, perpendicular to surface of lens) when entering a more dense medium.

Note, however, that this direction of bend changes from down (with the top ray) to up with the bottom ray. This is due to the geometry of the lens. Look at the picture to make sure that this makes sense.


The FOCAL LENGTH (f) of a lens (or curved mirror) where the light rays would intersect, but ONLY IF THEY WERE INITIALLY PARALLEL to each other. Otherwise, they intersect at some other point, or maybe not at all!

The location of images can be predicted by a powerful equation:

1/f = 1/di + 1/do

In this equation, f is the theoretical focal length (determined by the geometry of the lens or mirror), do is the distance between the object and lens (or mirror) and di is the distance from lens (or mirror) to the formed image.

We find several things to be true when experimenting with lenses. If the object distance (do) is:

greater than 2f -- the image is smaller
equal to 2f -- the image is the same size as the object (and is located at a di equal to 2f)
between f and 2f -- the images is larger
at f -- there is NO image
within f -- the image is VIRTUAL (meaning that it can not be projected onto a screen) and it appears to be within the lens (or mirror) itself

If an image CAN be projected onto a screen, the image is REAL. Convex lenses (fatter in the middle) and concave mirrors (like the inside of a spoon) CAN create real images - the only cases where there are no images for convex lenses or concave mirrors are when do = f, or when do < f. In the first case, there is NO image at all. In the second case, there is a magnified upright virtual image within the lens.

Concave lenses (thinner in the middle) NEVER create real images and ONLY/ALWAYS create virtual images. This is also true for convex mirrors (like the outside of a spoon, or a convenience store mirror).

Play around with this applet:

http://www.physics.metu.edu.tr/~bucurgat/ntnujava/Lens/lens_e.html

Convex lenses (which are defined to have a positive focal length) are similar to concave mirrors.

Concave lenses (which are defined to have a negative focal length) are similar to convex mirrors.


This is a bit more complicated, but here are some images and information for mirrors:

http://www.physicstutorials.org/home/optics/reflection-of-light/curved-mirrors/concave-mirrors

Test topics

Conservation of energy - the basic idea
Simple harmonic motion
Properties of a wave
harmonics on a string (lambda = 2L/n)
harmonic number and drawing waves
wave speed (v = f lambda)
for light, c = f lambda
types of waves: mechanical, EM
organ pipes, open on both ends (and closed on one end)
music - the basics (octaves, how to get to the next note on the piano)
EM spectrum
Doppler effect, red shift, blue shift
reflection
refraction: index of refraction, bending of light
total internal reflection

Total Internal Reflection

We've looked at light going from air (or a vacuum) into water (or glass, etc.). Now imagine it the other way around: going from water into air. Clearly, the light ray will be bent AWAY from the normal line. Several rays are shown in this image - the normal lines are indicated by a dotted line.

As the light ray hits the water surface at a greater and greater angle, eventually the light ray can NOT leave the water. That is, it "skates" along the surface (angle equal to 90 degrees). Any angle greater than this so-called "critical angle" results in the light reflecting BACK INTO the water. This phenomena is called: TOTAL INTERNAL REFLECTION

It is the secret behind fiber optics.

Refraction, in gross gory detail

Consider a wave hitting a new medium - one in which is travels more slowly. This would be like light going from air into water. The light has a certain frequency (which is unchangeable, since its set by whatever atomic process causes it to be emitted). The wavelength has a certain amount set by the equation, c = f l, where l is the wavelength (Greek symbol, lambda).

When the wave enters the new medium it is slowed - the speed becomes lower, but the frequency is fixed. Therefore, the wavelength becomes smaller (in a more dense medium).

Note also that the wave becomes "bent." Look at the image above: in order for the wave front to stay together, part of the wave front is slowed before the remaining part of it hits the surface. This necessarily results in a bend.

The general rule - if a wave is going from a lower density medium to one of higher density, the wave is refracted TOWARD the normal (perpendicular to surface) line. See picture above.

Reflection and Refration

Reflection - light "bouncing" off a reflective surface. This obeys a simple law, the law of reflection!

The incident (incoming) angle equals the reflected angle. Angles are generally measured with respect to a "normal" line (line perpendicular to the surface).

Note that this works for curved mirrors as well, though we must think of a the surface as a series of flat surfaces - in this way, we can see that the light can reflect in a different direction, depending on where it hits the surface of the curved mirror. More to come here.

Refraction is much different. In refraction, light enters a NEW medium. In the new medium, the speed changes. We define the extent to which this new medium changes the speed by a simple ratio, the index of refraction:

n = c/v

In this equation, n is the index of refraction (a number always 1 or greater), c is the speed of light (in a vacuum) and v is the speed of light in the new medium.

The index of refraction for some familiar substances:

vacuum, defined as 1

air, approximately 1

water, 1.33

glass, 1.5

polycarbonate ("high index" lenses), 1.67

diamond, 2.2

The index of refraction is a way of expressing how optically dense a medium is. The actual index of refraction (other than in a vacuum) depends on the incoming wavelength. Different wavelengths have slightly different speeds in (non-vacuum) mediums. For example, red slows down by a certain amount, but violet slows down by a slightly lower amount - meaning that red light goes through a material (glass, for example) a bit faster than violet light. Red light exits first.

In addition, different wavelengths of light are "bent" by slightly different amounts. This is trickier to see. We will explore it in the next blog entry.

http://www.physicsclassroom.com/class/refln/

worthwhile text reading

Chapter 12, 12.1-12.4, 12.7-12.11

Chapter 13, 13.1

Chapter 14, 14.1-14.5